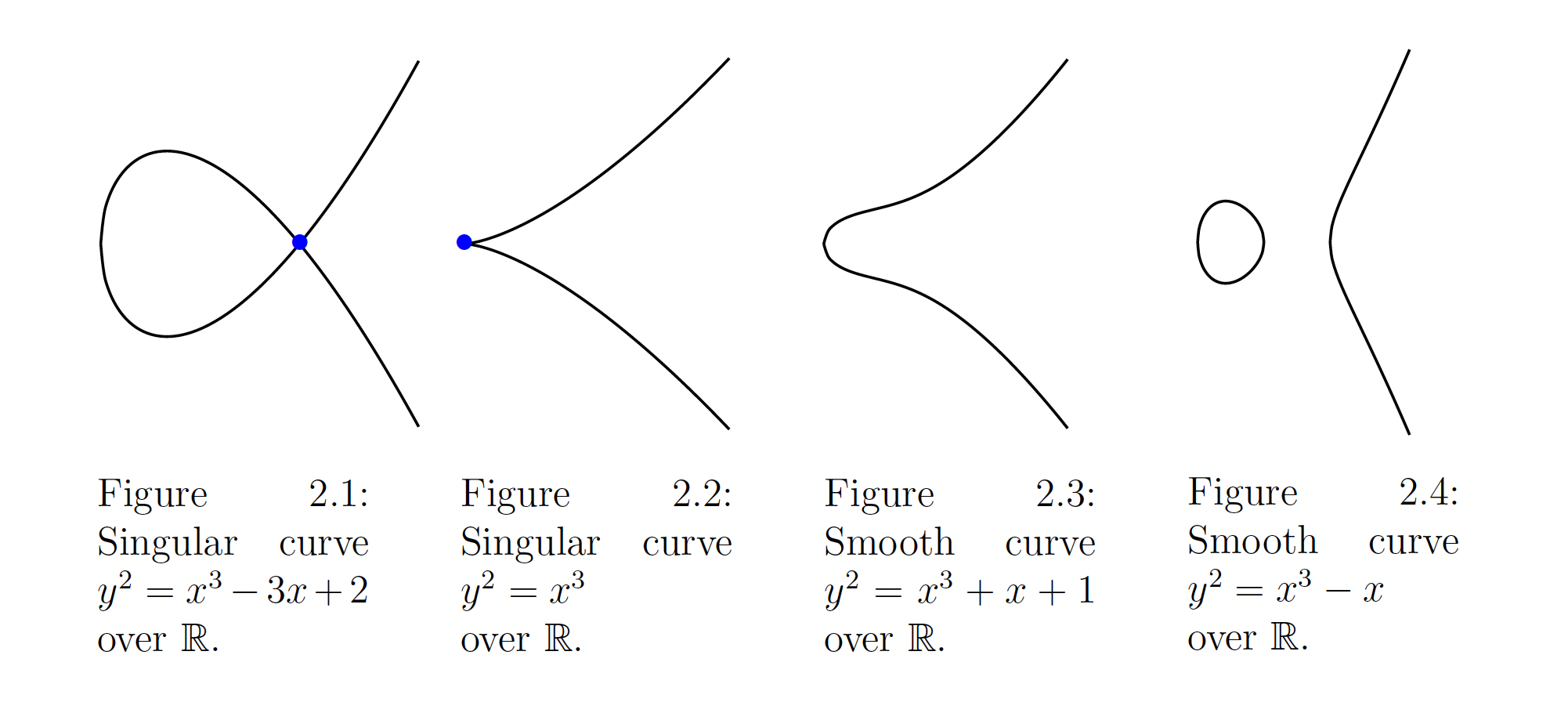
The Weierstrass normal form of elliptic curves (in fields with characteristic != 2 and != 3) $y^2 = x^3 + ax + b$ over $Z_p$ field has found many applications in cryptography. But this curve form has also two types: non-singular ( that can be used in crypto) and singular (that can’t). Let’s take a look why singular curves causes problems in cryptography.
Singular curves is the curves where discriminant is equal to zero, so $4a^3 + 27b^2 = 0$
In such cases, this curve can be represented in two forms:
-
$y^2 = x^3$ (when there is a triple root 0) where using mapping $(x, y) \rightarrow \frac{x}{y}$ it gives an isomorphism to additive group ( with same order $p$) where discrete logarithm is trivial.
-
$y^2 = x^2(x + c)$ (when there is a double root 0) where using mapping $(x, y) \rightarrow \frac{y + xc}{y - xc}$ it gives an isomorphism to multiplicative group (with order $p^2$) where discrete logarithm problem is easy to solve for default elliptic key sizes.
This both cases are perfectly overviewed in Section 2.10 of Washington’s Elliptic Curves: Number Theory and Cryptography.
Here is an example how to solve discrete logarithm problem for such curves.