Commitment
Vortex has much in common with Ligero (frankly speaking, it has been built using Ligero idea). So, imagine we have a list of polynomials $f_0,\dots,f_{k-1}$. We want to commit them and evaluate at the same point at the same time. We describe each polynomial as vector $a_i$ where
\[f_i(x) = \sum_{j=0}^{n-1} x^j\cdot a_{i,j}\]For simplicity, let’s define the interpolation function $Int$ that works as follows (it takes the vector elements as polynomial coefficients and evaluates it at point $x$):
\[Int_{a_i}(x) = f_i(x)\]Then, we organize these vectors into the matrix $W \in \mathbb{F}^{k\times n}$.
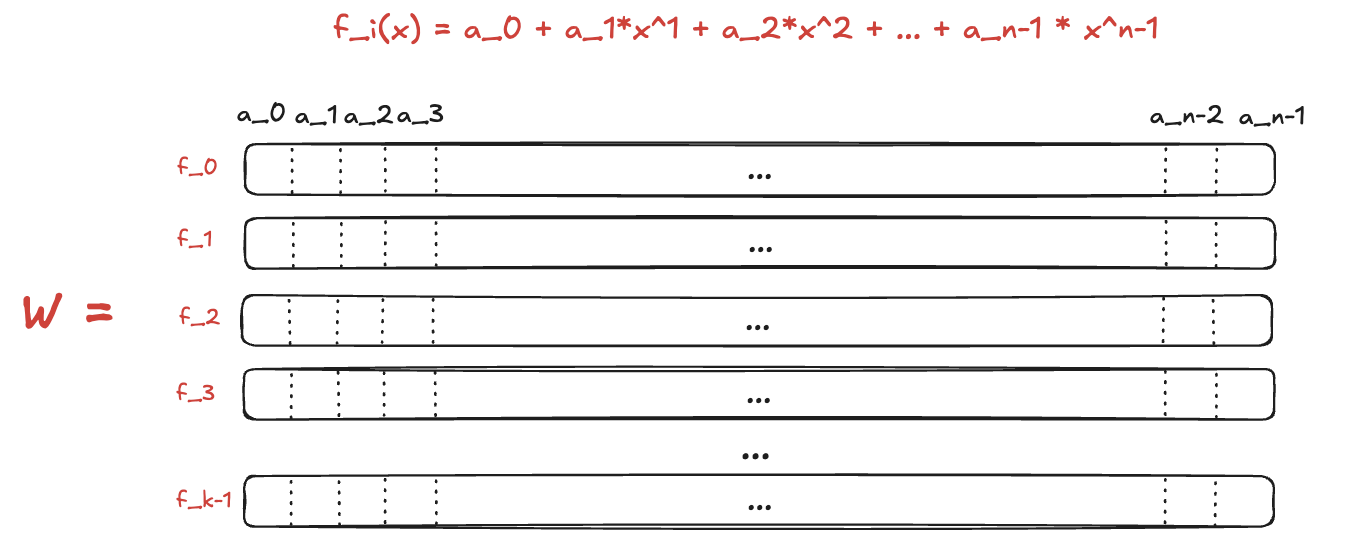
Same as in Ligero, we extend our matrix with additional columns by replacing each word $a_i$ with its codeword $a_i’$, resulting in a matrix $W’ \in \mathbb{F}^{k\times m}$, where $m > n$.
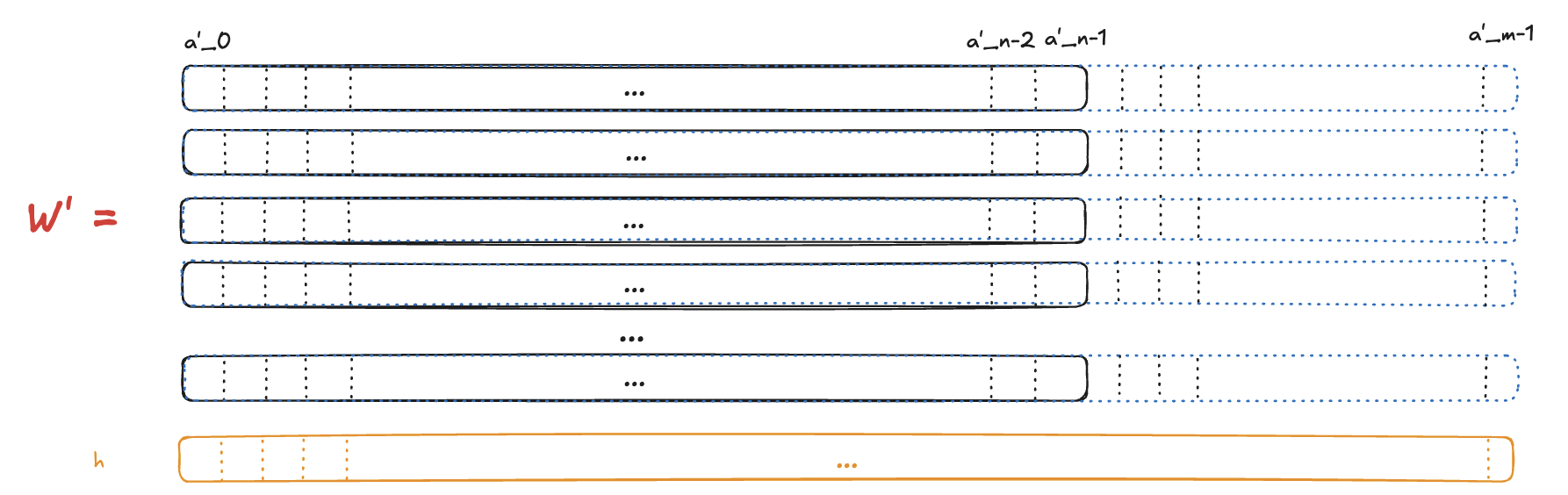
Then we hash each column, receiving $m$ values of $h_i$ — we will use these values as our commitment to the polynomials
$f_i$.
Open
Given input $r$ from the verifier, the prover responds with values $y_0,\dots,y_{k-1}$ where
\[y_i = f_i(x)\]Prove & Verification
- The verifier samples a challenge $\beta$
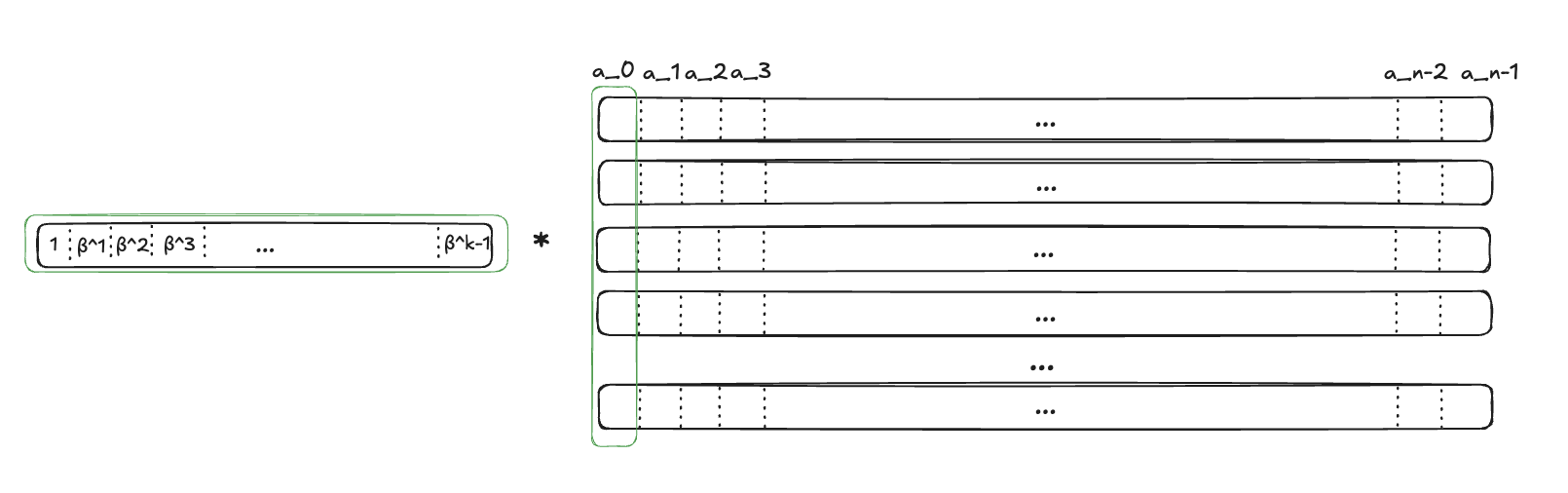
- The prover responds with $u = B\cdot W$, where $B = (1, \beta, \beta^1,\dots,\beta^{k-1})$. Note that naturally, each
element in $u$ equals to the sum of corresponding polynomials’ coefficients over corresponding weight – polynomial
$i$ will be multiplied by $\beta^i$.
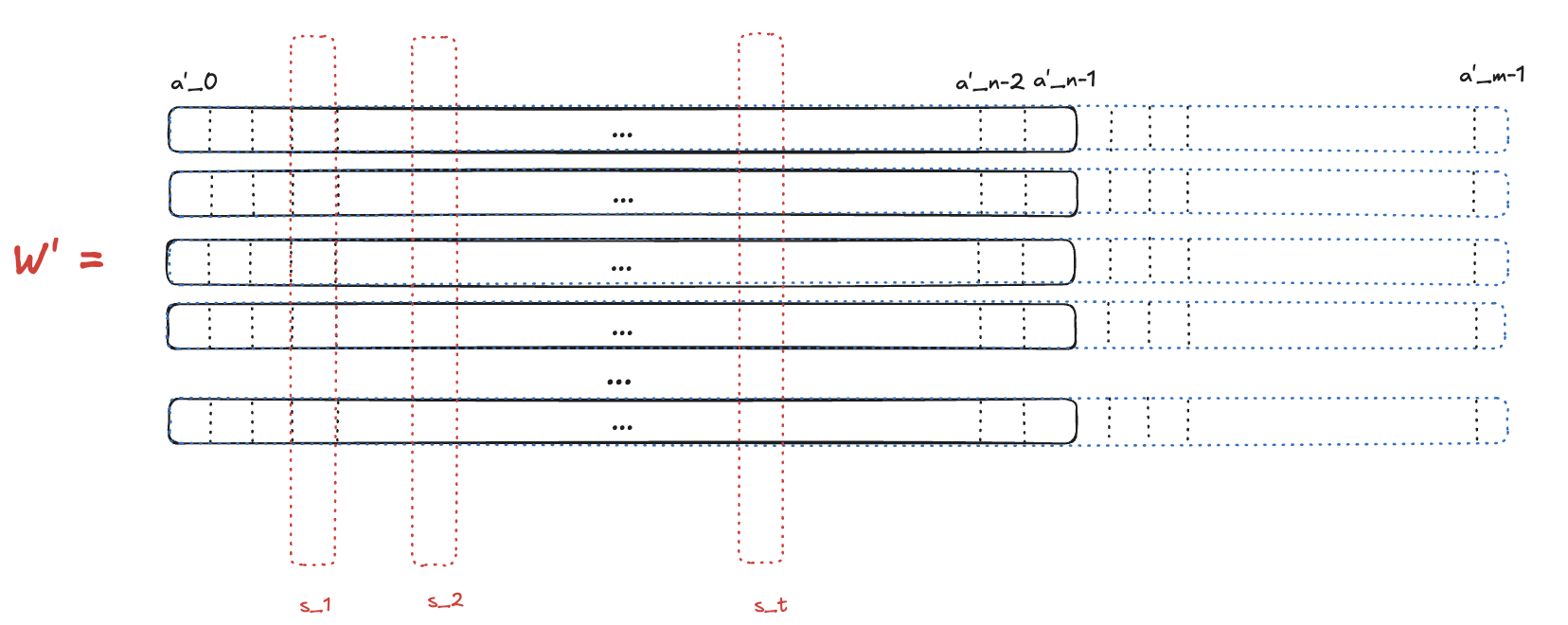
- Then, the verifier samples $t$ indexes $q_1,\dots,q_t$ where $q_i \in [m]$
- The prover opens the corresponding columns $s_1,\dots,s_t$ from the matrix $W’$
- The verifier computes the Reed-Solomon encoding of $u$ named $u’$.
- The verifier checks:
- $hash(s_i) == h_{q_i}$ for each $i\in [t]$
- $B\cdot s_i == u’_{q_i}$ → this follows from the linearity of Reed-Solomon
- The verifier checks that $Int_u(x) = B\cdot y$. This check follows from the following observation: $a\cdot Int_c(x) =
Int_{a\cdot c}(x)$, so:
- $1 \cdot Int_{w_0}(x) = 1 \cdot y_0$ → $Int_{u_0}(x) = 1 \cdot y_1$
- $\beta \cdot Int_{w_1}(x) = \beta \cdot y_1$ → $Int_{u_1}(x) = \beta \cdot y_1$
- $\beta^2 \cdot Int_{w_2}(x) = \beta^2 \cdot y_2$ → $Int_{u_2}(x) = \beta^2 \cdot y_2$
- etc.
The parameter $t$ is selected according to the security parameters.