Ligero for multilinear polynomials

Commitment

To commit to an $\ell$-variate multilinear polynomial $f(x)$ we assume it (as equivalent) to represent as a list of elements where each element at the position $i$ equals to $f(\tilde{i})$ where $\tilde{i}$ represents a bit string equivalent to the $i$ value. Then, we reorganize this list into the matrix $M$ of size $2^{{\ell }_0}\times 2^{{\ell }_1}$ in such a way that:

$$f(\tilde{i})=M[{\tilde{i}}_0][{\tilde{i}}_1]$$

where

$$\tilde{i}={\tilde{i}}_0||{\tilde{i}}_1$$

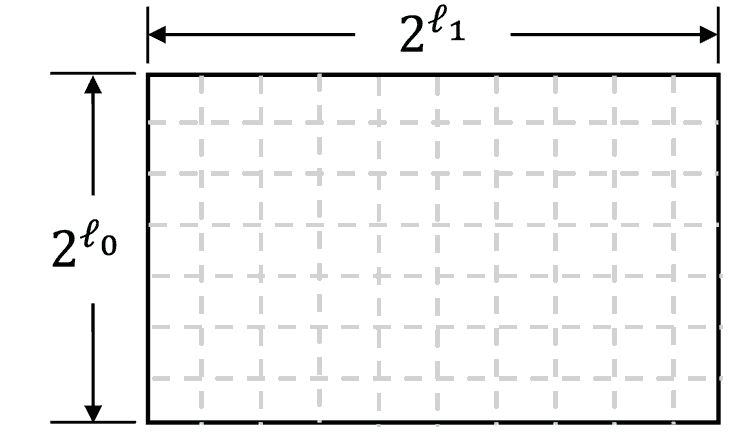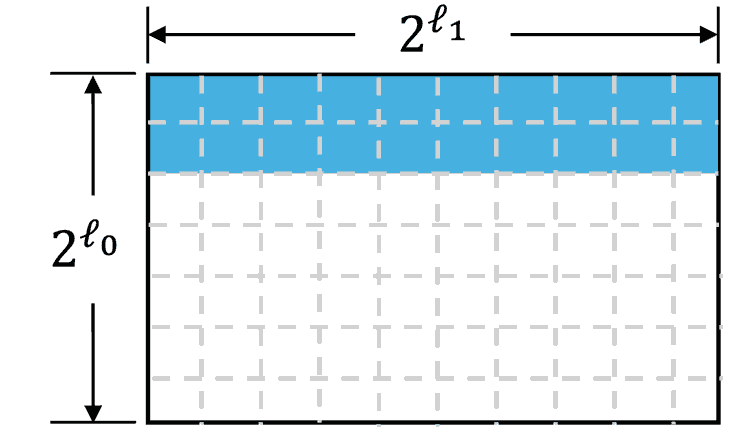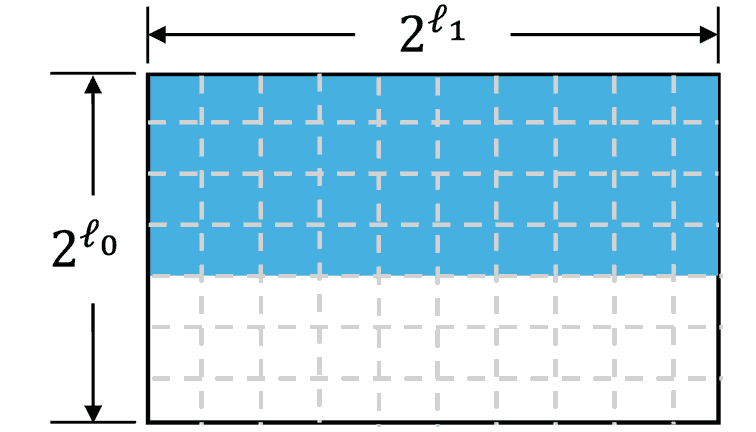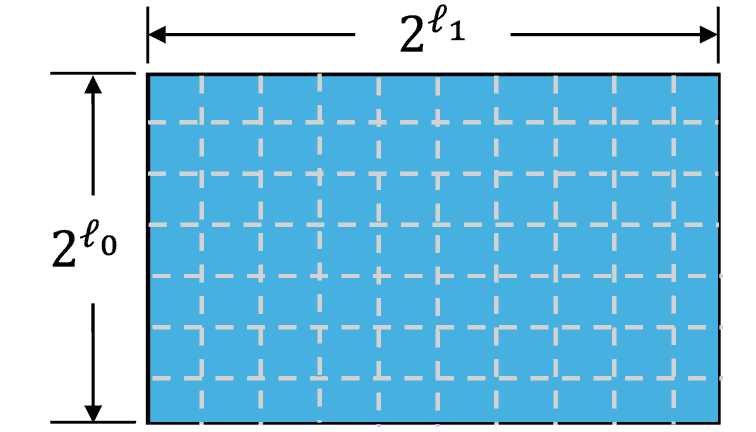
Then, for each row, we replace it with its error-correcting code representation, assuming that the matrix will become bigger — it will have size $2^{{\ell }_0}\times 2^{{\ell }_2}$ where ${\ell }_2>{\ell }_1$

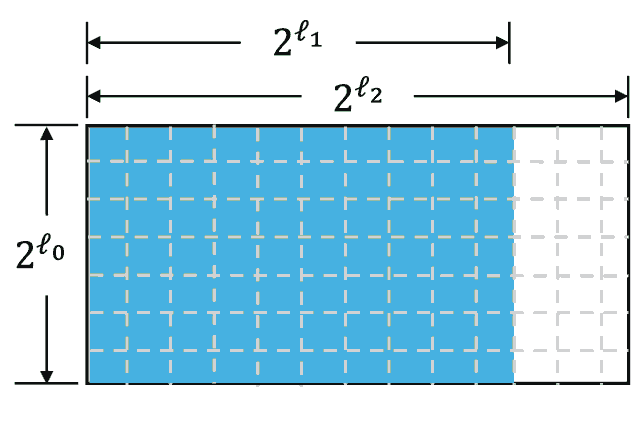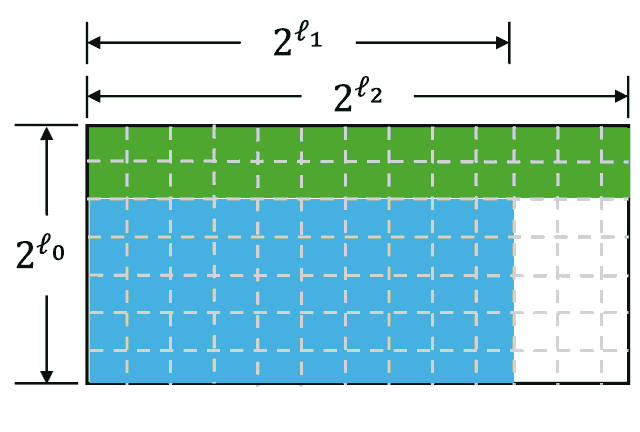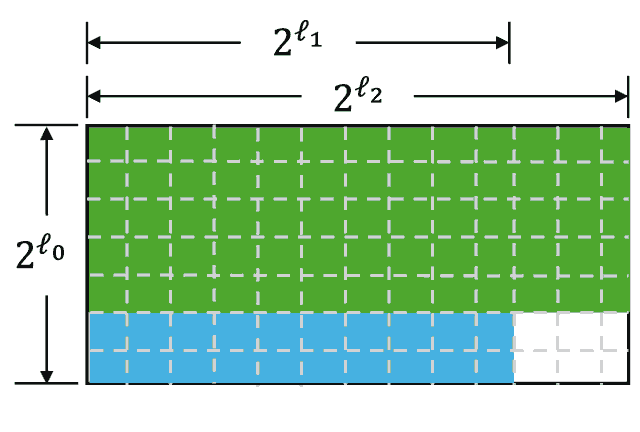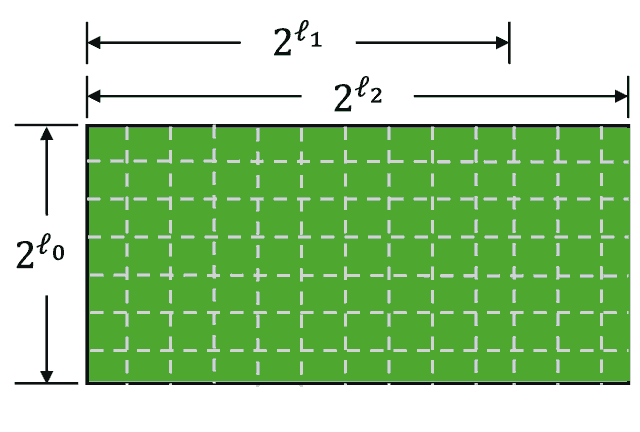
The commitment to its matrix will be a Merkle tree, where each leaf will contain a corresponding column. For example:

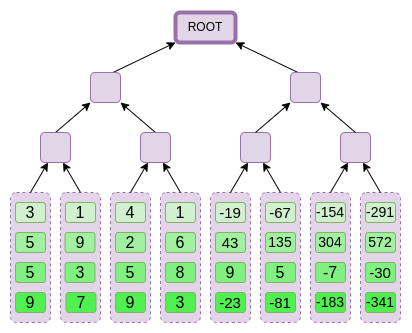
Openning

To open the polynomial value at a point $r$ the prover splits it into two parts $r_1$ and $r_2$ of sizes ${\ell }_1$ and ${\ell }_2$. Then, the prover opens the value $M[r_1][r_2]$.

Proving and Verification

To prove that the opening $M[r_1][r_2]$ corresponds to the commitment (Merkle tree hash), the prover goes through the following steps:

• The prover selects a row $w=M[r_1]$ and shares it.
• The verifier checks that the element on the position $r_2$ in the row $w$ equals $M[r_1][r_2]$.
• The verifier evaluates an error correcting code of $w$.
• The verifier selects several columns (in the encoded matrix) and asks the prover to open it with the corresponding Merkle proofs.
• The verifier selects the corresponding elements from these columns (on the positions $r_1$) and checks the equality with the corresponding elements in the encoded row $w$.

Note, that this is a non-zero-knowledge version of the protocol. While sharing the opened row $w$ we share the additional private information besides the requested opening so the commitment protocol does not own a perfect hiding property.

In the section 4.6 of https://eprint.iacr.org/2022/1608.pdf the author describes how to make this protocol zero-knowledge.

To achieve this, we add an additional random row $u$ into the matrix (WLOG append it downside). The encoded version of this row will also be committed. Then, we suppose to share $w=M[r_1]+u$ with verifier. During the verification phase, the verifier becomes able to check that the encoded elements of $w$ are valid by adding last column element to the $r_1$ element.

To prove that the opening $M[r_1][r_2]$ corresponds to the commitment (Merkle tree hash), the prover goes through the following steps:

• The prover shares the $u[r_2]$ value.
• The prover selects a row $w=M[r_1]$ and shares it.
• The verifier checks that the element on the position $r_2$ in the row $w$ equals $M[r_1][r_2]+u[r_2]$.
• The verifier evaluates an error correcting code of $w$, namely $ECC(w)$.
• The verifier selects several columns (in the encoded matrix) and asks the prover to open it with the corresponding Merkle proofs.
• For the column $c$ with index $k$ the verifier checks that $c[r_1]=ECC(w)[k]+c.last()$.