Vortex polynomial commitment

Commitment

Vortex has much in common with Ligero (frankly speaking, it has been built using Ligero idea). So, imagine we have a list of polynomials $f_1,\dots ,f_m$. We want to commit them and evaluate at the same point at the same time. So, leveraging the Reed-Solomon’s evaluation domain $D$ we describe each polynomial as vector $w_i$ where the interpolation of $w_i$ equals to the $f_i$:

$$\forall x\in D:f_j(x)=w_{i,j}$$

For simplicity, let’s define the interpolation function $Int$ that works as follows:

$$In{t}_{w_i}(x)=f_i(x)$$

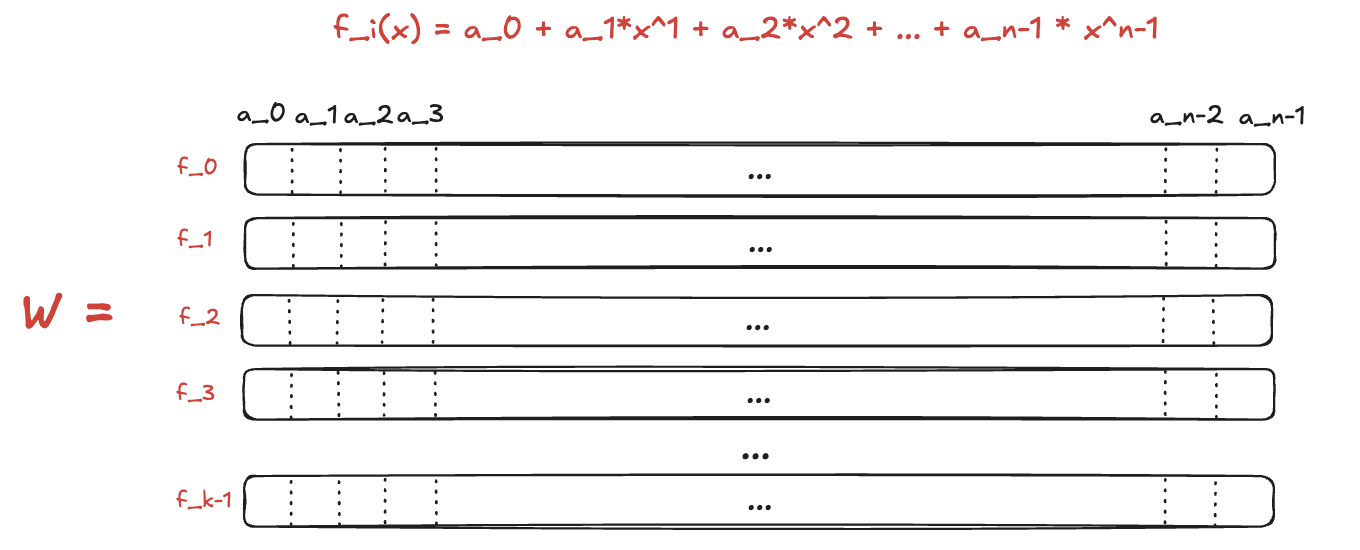
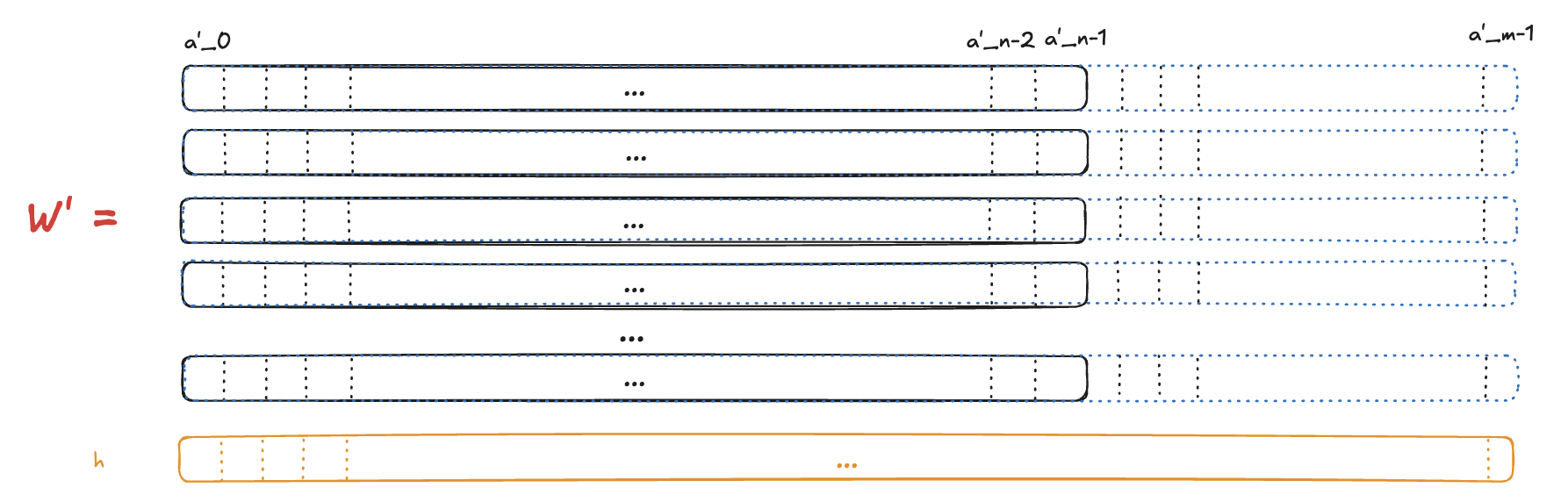
Then, we organize these vectors into the matrix $W\in {\mathbb{F}}^{m\times k}$. Same as in Ligero, we extend our matrix with additional columns by replacing each word $w_i$ with its codeword, resulting in a matrix $W^{\prime }\in {\mathbb{F}}^{m\times n}$, where $n>k$.

Then we hash each column, receiving $n$ values of $h_i$ — we will use these values as our commitment to the polynomials $f_i$.

Open

Given input $r$ from the verifier, the prover responds with values $y_1,\dots ,y_m$ where

$$y_i=f_i(x)$$

Prove & Verification

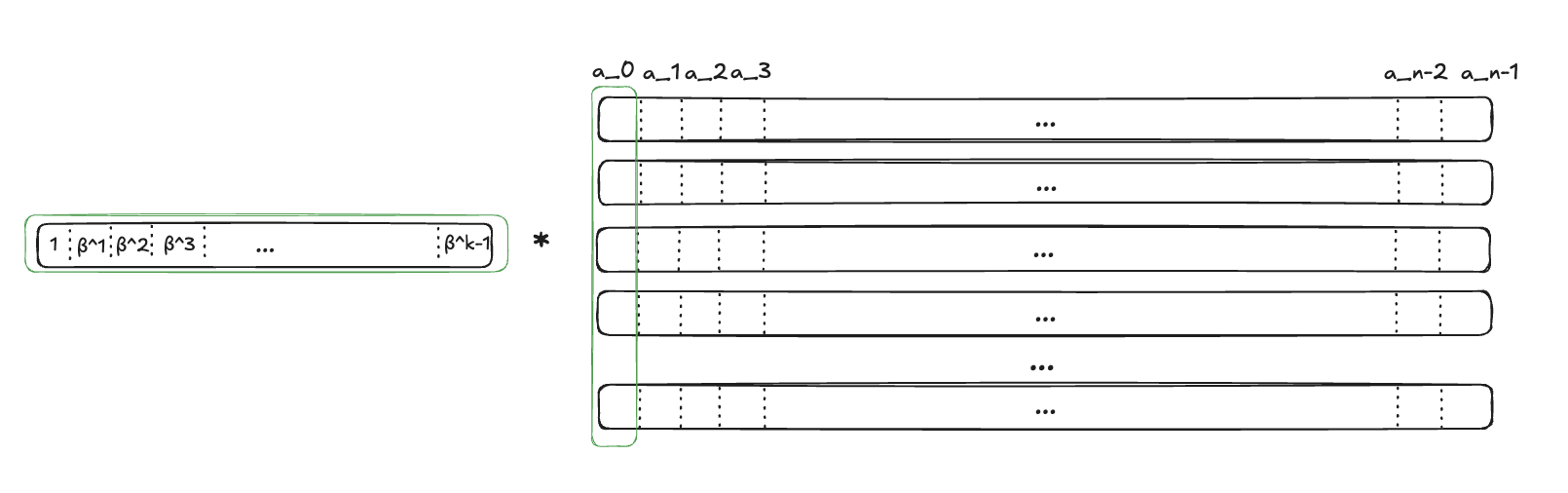
• The verifier samples a challenge $\beta$
• The prover responds with $u=B\cdot W$, where $B=(1,\beta ,{\beta }^1,\dots ,{\beta }^{m-1})$
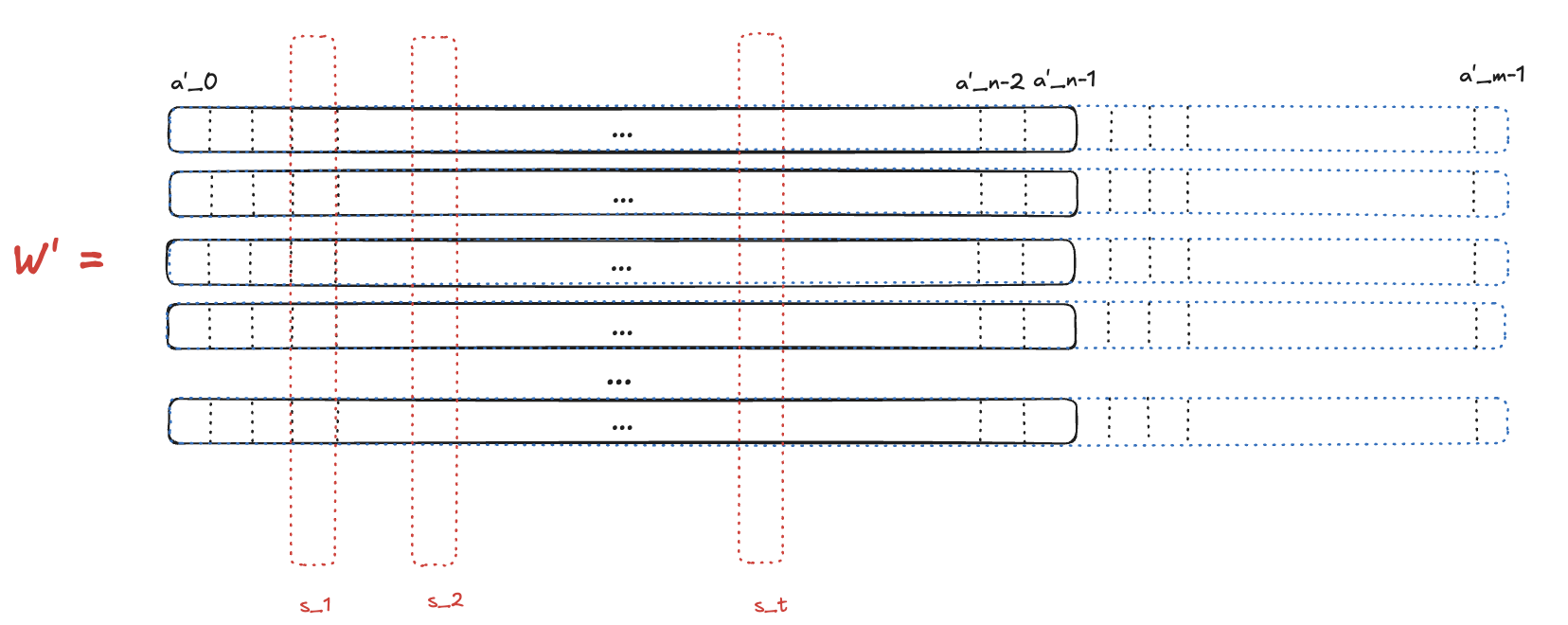
• Then, the verifier samples $t$ indexes $q_1,\dots ,q_t$ where $q_i\in [n]$
• The prover opens the corresponding columns $s_1,\dots ,s_t$ from the matrix $W^{\prime }$
• The verifier computes the Reed-Solomon encoding of $u$ named $u^{\prime }$
• The verifier checks:
  • $hash(s_i)==h_{q_i}$ for each $i\in [t]$
  • $B\cdot s_i==u_{q_i}^{\prime }$ → this follows from the linearity of Reed-Solomon
• The verifier checks that $In{t}_u(x)=B\cdot y$. This check follows from the following observation: $a\cdot In{t}_c(x)=In{t}_{a\cdot c}(x)$, so:
  • $1\cdot In{t}_{w_0}(x)=1\cdot y_0$ → $In{t}_{u_0}(x)=1\cdot y_1$
  • $\beta \cdot In{t}_{w_1}(x)=\beta \cdot y_1$ → $In{t}_{u_1}(x)=\beta \cdot y_1$
  • ${\beta }^2\cdot In{t}_{w_2}(x)={\beta }^2\cdot y_2$ → $In{t}_{u_2}(x)={\beta }^2\cdot y_2$
  • etc.

The parameter $t$ is selected according to the security parameters.